Transformações em Imagens Vetoriais no Plano

Afluentes: Computação Gráfica

Representação

O plano é um espaço bidimensional composto de dois vetores, x e y. Para representar elementos vetoriais no plano, é necessário primeiramente representar cada ponto (x, y) ligados por linhas.

Por exemplo, se tivermos um triângulo, composto de três pontos e linhas ligando cada um dos pontos, então teremos:

Ponto {
	Real x
	Real y
}

Triangulo = Vetor [3] Ponto

Triangulo.Ponto[0]( 5, 10);
Triangolo.Ponto[1](10,  5);
Triangulo.Ponto[2](15, 10);

j = 1;
Para i = 0 até 2 Fazer
	j = i + 1;
	Se j > 2
		Então j = 0
	Fim se
	Desenhar_linha(
		Triangulo[i].Ponto.x, Triangulo[i].Ponto.y,
		Triangulo[j].Ponto.x, Triangulo[j].Ponto.y)
Fim para

Figura 1: Representação de um triângulo no Plano.

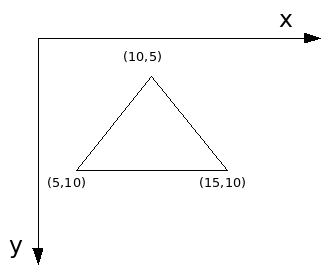
O código no final dessa página apresenta a estrutura de um triângulo com as operações de transformação no plano: translação, escala e rotação.

Transformações

As transformações são operações feitas nos objetos existentes, no plano bidimensional nesse caso, de forma que eles sejam modificados. Existem diversos tipos de operações, mas veremos apenas as transformações de translação, escala e rotação. Para um objeto com n pontos, as operações de transformações devem ser aplicadas à todos os pontos.

Translação

A translação no plano é a operação que move determinado objeto de um local à outro no no espaço bidimensional. A operação da translação ocorre com a soma da matriz de translação com todos os pontos do objeto. A matriz de translação é uma matriz horizontal de 1 por 2 com os elementos T_x e T_y:

${\begin{pmatrix}Tx&Ty\end{pmatrix}}$

tal que:

Tx é a translação na horizontal e
Ty é a translação na vertical.

Logo, a fórmula matemática da operação de translação se caracteriza pela soma da matriz bidimensional horizontal de 1 por 2 contendo x e y de entrada somada a matriz bidimensional horizontal de 1 por 2 de Tx e Ty:${\begin{pmatrix}x&y\end{pmatrix}}+{\begin{pmatrix}Tx&Ty\end{pmatrix}}$tal que, com a soma das matrizes temos:

x' = x + Tx
y' = y + Ty

Sendo que x' e y' são os novos valores de x e y aplicados ao ponto transladado.

Algoritmo

Baseado na matriz e na fórmula para a operação de translação no plano, o algoritmo para esta operação fica da seguinte maneira:

Entrada Tx e Ty

Para i = 0 Até Quantidade_de_pontos Fazer
	Ponto[i].x = Ponto[i].x + Tx
	Ponto[i].y = Ponto[i].y + Ty
Fim para

Ou seja, conforme já comentamos, a operação é executada em todos os pontos do elemento.

Exemplo

Agora imagine que vamos executar a operação de translação no nosso triângulo (Figura 1). Considere que vamos executar a operação de translação com os seguintes valores de Tx e Ty respectivamente (-2, 7). Então teremos que:

Ponto[0].x = Ponto[0].x + Tx = 5 + (-2) = 3
Ponto[0].y = Ponto[0].y + Ty = 10 + 7 = 17

Ponto[0].x = Ponto[0].x + Tx = 10 + (-2) = 8
Ponto[0].y = Ponto[0].y + Ty = 5 + 7 = 12

Ponto[0].x = Ponto[0].x + Tx = 15 + (-2) = 13
Ponto[0].y = Ponto[0].y + Ty = 10 + 7 = 17

Logo, nossos pontos passarão a ser:

Pontos (3, 17),	(8, 12) e (13, 17)

Gerando uma nova imagem com o elemento Triângulo em uma nova posição.

Figura 2: O Triângulo após a operação de translação.

Escala

A operação de escala no plano é a operação que modifica o tamanho do objeto.

A matriz de transformação escalar é uma matriz quadrada de 2 por 2 com os elementos da primeira linha Sx e 0 e da segunda linha 0 e Sy, sendo que Sx e Sy conforme apresentado abaixo:

${\begin{pmatrix}Sx&0\\0&Sy\end{pmatrix}}$

tal que:

Sx : é a modificação da escala na horizontal e
Sy : é a modificação da escala na vertical.

Logo, a fórmula matemática da operação de escala é a multiplicação da matriz horizontal de 1 por 2 multiplicada pela matriz da escala descrita acima:

${\begin{pmatrix}x&y\end{pmatrix}}\cdot {\begin{pmatrix}Sx&0\\0&Sy\end{pmatrix}}$

tal que:

x = (x * Sx) + (y * 0) = x * Sx
y = (x * 0) + (y * Sy) = y * Sy

Algoritmo

Baseado na matriz e na fórmula para a operação de escala no plano, o algoritmo para esta operação fica da seguinte maneira:

Entrada Sx e Sy

Para i = 0 Até Quantidade_de_pontos Fazer
	Ponto[i].x = Ponto[i].x * Sx
	Ponto[i].y = Ponto[i].y * Sy
Fim para

A operação é executada em todos os pontos do elemento, assim como na operação de translação.

Exemplo

Agora imagine que vamos executar a operação de escala no nosso triângulo original (Figura 1). Considere que vamos executar a operação de escala com os seguintes valores de Sx e Sy respectivamente (0.5, 2). Então teremos que:

Ponto[0].x = Ponto[0].x * Sx =  5 * 0.5 =  2.5
Ponto[0].y = Ponto[0].y * Sy = 10 * 2   = 20

Ponto[0].x = Ponto[0].x * Sx = 10 * 0.5 =  5
Ponto[0].y = Ponto[0].y * Sy =  5 * 2   = 10

Ponto[0].x = Ponto[0].x * Sx = 15 * 0.5 =  7.5
Ponto[0].y = Ponto[0].y * Sy = 10 * 2   = 20

Logo, nossos pontos passarão a ser:

Pontos (2.5, 20), (5, 10) e (7.5, 20)

Gerando uma nova imagem com o elemento Triângulo com sua escala modificada.

Figura 3: O triângulo após a operação de translação.

Porém, temos um problema. Ao aplicar a escala, estamos modificando também a posição do nosso elemento. Para contornar o problema, devemos definir um ponto que será visto como o ponto de origem da figura, também chamado de pivô. Devemos salvar as informações do pivô, transladar a imagem para -pivô, executar a operação de escala e depois transladamos a imagem de volta com base em +pivô.

Neste caso, pegaremos o primeiro ponto (ponto 0) como pivô do objeto para mostrar o exemplo acima agora usando a operação sobre o pivô. Veja bem, uma figura pode ter um ponto específico que é apenas o pivô dela e não serve para representação visual. Dessa forma, podemos colocar o pivô no centro da imagem para que possamos escalar ou rotacionar ela com base ao seu centrou ou até colocar esse pivô am algum ponto conveniente, como por exemplo a ponta de um braço para transformações de animação, criando um esqueleto de pivôs conectados que são influenciados pelos seus pivôs pais.

Agora com o uso do pivô, nosso algoritmo fica da seguinte forma:

Entrada Sx e Sy

Pivot = Ponto[0];

Transladar(-Pivot.x, -Pivot.y);

Para i = 0 Até Quantidade_de_pontos Fazer
	Ponto[i].x = Ponto[i].x * Sx
	Ponto[i].y = Ponto[i].y * Sy
Fim para

Transladar(Pivot.x, Pivot.y);

Agora com essa operação de translação usando o pivot negativo, temos os seguintes pontos:

Pontos = (0, 0), (5, -5) e (10, 0)

Veja que nosso pivô é colocado na origem do nosso plano, no ponto (0, 0). Dessa forma todas as operações são com base no ponto de origem.

Figura 4: Transladando para a origem utilizando o pivô.

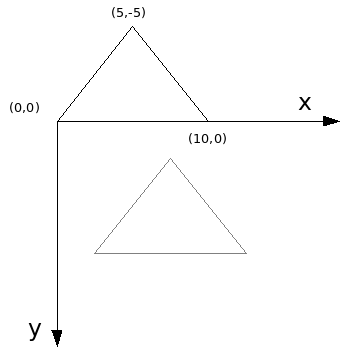
Só então aplicamos a operação de Escala, resultando os seguintes pontos:

Pontos = (0, 0), (2.5, -10) e (5, 0)

Figura 5: Operação de Escala.

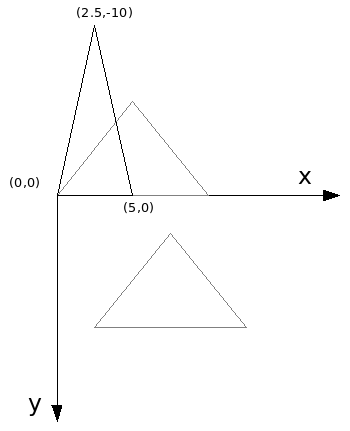
Depois disso então movemos de volta os pontos para o ponto de origem do objeto conforme a localização original do pivô, armazenada anteriormente. Obtemos então os seguintes pontos:

Pontos = (5, 10), (7.5, 0) e (10, 10)

Figura 6: Transladando de volta ao ponto de referência, pivô.

Rotação

A rotação, no plano, é a operação que rotaciona determinado objeto no espaço bidimensional. A operação de rotação ocorre com a multiplicação da matriz de Rotação com todos os pontos do objeto. A matriz de rotação é a seguinte:

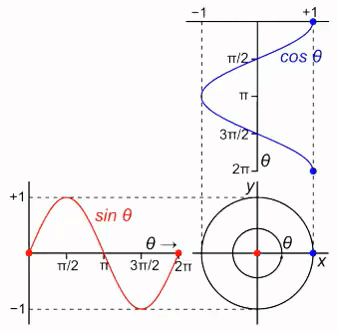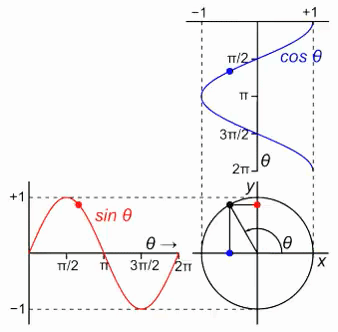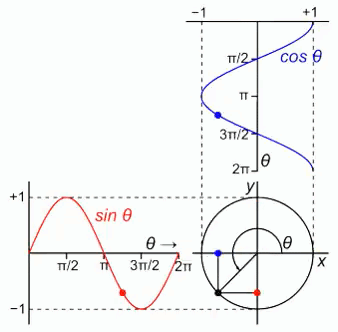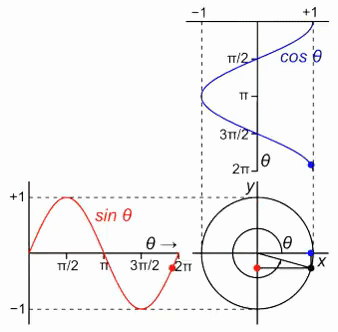
A matriz de rotação é uma matriz quadrada de dois por dois com os elementos a primeira linha sendo cosseno do ângulo e seno do ângulo, e da segunda linha menos seno do ângulo e cosseno do ângulo, sendo que o ângulo é simbolizado pela letra grega teta.

${\begin{pmatrix}\cos(\theta )&\sin(\theta )\\-\sin(\theta )&\cos(\theta )\\\end{pmatrix}}$

tal que:

θ é o ângulo, em radianos, que se quer rotacionar o objeto,
sin é a operação do seno sobre o ângulo e
cos é a operação do cosseno sobre o ângulo.

Logo, a fórmula matemática da operação de rotação é a multiplicação da matriz horizontal de um por dois dos pontos x e y pela matriz quadrada da rotação apresentada acima:

${\begin{pmatrix}x&y\end{pmatrix}}\cdot {\begin{pmatrix}\cos(\theta )&\sin(\theta )\\-\sin(\theta )&\cos(\theta )\\\end{pmatrix}}$

tal que:

x' = (x * cos(θ)) + (y * -sin(θ))
y' = (x * sin(θ)) + (y * cos(θ))

Observe que agora temos x' e y'. Isso por que em ambas as oeprações estamos utilizando o x e y originais. Se modificarmos o x na primeira operação, na segunda ele já vai estar modificado, o que distorce o elemento. A solução é criar variáveis auxiliares para não alterar os valores originais até o término do processo.

Outro ponto importante é que, assim como na escala, devemos transladar nosso objeto para o ponto de origem do espaço, baseando-se em um pivot do elemento.

Algoritmo

Baseado na matriz e na fórmula para a operação de escala no plano, o algoritmo para esta operação fica da seguinte maneira:

Entrada ang

Pivot = Ponto[0];

Transladar (-Pivot.x, -Pivot.y)

Para i = 0 Até Quantidade_de_pontos Fazer
	xAux = (Ponto[i].x * cos(ang)) + (Ponto[i].y * -sen(ang))
	yAux = (Ponto[i].x * sen(ang)) + (Ponto[i].y *  cos(ang))
	Ponto[i].x = xAux
	Ponto[i].y = yAux
Fim para

Transladar (Pivot.x, Pivot.y)

A operação é executada em todos os pontos do elemento, assim como na operação de translação e na escala.

Código em Python

Juntando tudo em um código python, temos o script abaixo.

import pygame
import copy
from math import sin, cos, radians

class Ponto:
    def __init__(self, x, y):
        self.x = x
        self.y = y

def draw(tela, figura, cor):
    size = len(figura)
    for i in range(size):
        j = i + 1
        if j >= size:
            j = 0
        pygame.draw.line(tela, cor,
            (figura[i].x, figura[i].y),
            (figura[j].x, figura[j].y), 1)

def translacao(figura, tx, ty):
    for i in range(len(figura)):
        figura[i].x = figura[i].x + tx
        figura[i].y = figura[i].y + ty

def escala(figura, sx, sy):
    pivo_x = figura[0].x
    pivo_y = figura[0].y
    translacao(figura, -pivo_x, -pivo_y)
    for i in range(len(figura)):
        figura[i].x = figura[i].x * sx
        figura[i].y = figura[i].y * sy
    translacao(figura, pivo_x, pivo_y)

def rotacao(figura, ang):
    ang = radians(ang)  # o angulo precisa ser em radianos
    pivo_x = figura[0].x
    pivo_y = figura[0].y
    translacao(figura, -pivo_x, -pivo_y)
    for i in range(len(figura)):
        x2 = (figura[i].x * cos(ang)) + (figura[i].y * -sin(ang))
        y2 = (figura[i].x * sin(ang)) + (figura[i].y *  cos(ang))
        figura[i].x = x2
        figura[i].y = y2
    translacao(figura, pivo_x, pivo_y)

pygame.init()
tela = pygame.display.set_mode((800, 600))
pygame.display.set_caption("Triângulo")

triangulo = [
    Ponto(200, 250),
    Ponto(300, 150),
    Ponto(400, 250)
]

t2 = copy.deepcopy(triangulo)
t3 = copy.deepcopy(triangulo)
t4 = copy.deepcopy(triangulo)

translacao(t2, 20, 40)
escala(t3, 0.5, 1.6)
rotacao(t4, 90)

rodando = True
while rodando:
    for evento in pygame.event.get():
        if evento.type == pygame.QUIT:
            rodando = False
    tela.fill((255, 255, 255))  # Fundo branco
    draw(tela, triangulo, (255, 0, 0))
    draw(tela, t2, (0, 0, 255))
    draw(tela, t3, (0, 0, 255))
    draw(tela, t4, (0, 0, 255))
    pygame.display.flip()
pygame.quit()

Para ver apenas o resultado de cada operação (t2: translação, t3: escala e t4: rotação) comente a linha draw das outras figura.