Mudanças entre as edições de "Geometria"
| (4 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
| − | + | Links Relacionados: [[Matemática e Física para Jogos]], [[Usabilidade, Desenvolvimento Web, Mobile e Jogos]] | |
= Introdução = | = Introdução = | ||
| Linha 10: | Linha 10: | ||
Na computação gráfica, utilizamos conceitos geométricos para modelar cenários, animar personagens e criar efeitos visuais. As principais ferramentas para isso são as coordenadas cartesianas, transformações geométricas e o uso de matrizes para manipulação de objetos. | Na computação gráfica, utilizamos conceitos geométricos para modelar cenários, animar personagens e criar efeitos visuais. As principais ferramentas para isso são as coordenadas cartesianas, transformações geométricas e o uso de matrizes para manipulação de objetos. | ||
| + | |||
| + | * Utilizamos escalares, pontos e vetores para representar quantidades, posições e direções. | ||
| + | * Através da combinação de operações sobre esses elementos podemos representar objetos geométricos e realizar o processamento necessário para a síntese de imagens. | ||
= Conceitos Básicos = | = Conceitos Básicos = | ||
| Linha 18: | Linha 21: | ||
* '''Polígonos''': formados por múltiplos segmentos. | * '''Polígonos''': formados por múltiplos segmentos. | ||
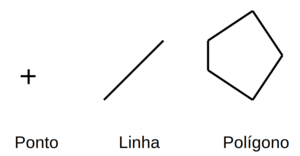
| − | [[Arquivo:Ponto linha poligono.png|centro|miniaturadaimagem|Elementos básicos da geometria.]] | + | [[Arquivo:Ponto linha poligono.png|centro|miniaturadaimagem|Elementos básicos da geometria representados por um ponto no espaço bidimensional, uma reta e um polígono com 5 lados não isométricos.]] |
== Coordenadas Cartesianas == | == Coordenadas Cartesianas == | ||
| Linha 27: | Linha 30: | ||
* Os eixos são usado para posicionar elementos gráficos. | * Os eixos são usado para posicionar elementos gráficos. | ||
| − | [[Arquivo:Grafico bidimensional coordenadas.png|centro|miniaturadaimagem|374x374px|Gráfico bidimensional.]] | + | [[Arquivo:Grafico bidimensional coordenadas.png|centro|miniaturadaimagem|374x374px|Gráfico bidimensional contendo o eixo x horizontal, o eixo y, vertical, e alguns pontos aleatórios distribuídos pelo gráfico com sua posição (x, y).]] |
A seguir temos um exemplo de programa em python, com o uso da biblioteca pygame, para criar linhas e polígonos. Não estamos desenhando um ponto porque visualmente seria apenas um pixel. Usamos os pontos para criar as linhas e demais elementos.<syntaxhighlight lang="python3"> | A seguir temos um exemplo de programa em python, com o uso da biblioteca pygame, para criar linhas e polígonos. Não estamos desenhando um ponto porque visualmente seria apenas um pixel. Usamos os pontos para criar as linhas e demais elementos.<syntaxhighlight lang="python3"> | ||
| − | |||
| − | |||
pygame.init() | pygame.init() | ||
| − | |||
screen = pygame.display.set_mode((500, 500)) | screen = pygame.display.set_mode((500, 500)) | ||
| − | |||
| − | |||
running = True | running = True | ||
while running: | while running: | ||
| Linha 44: | Linha 42: | ||
screen.fill((255, 255, 255)) | screen.fill((255, 255, 255)) | ||
| + | |||
# Desenhamos uma linha na tela, do ponto (30, 50) ao ponto (180, 200) | # Desenhamos uma linha na tela, do ponto (30, 50) ao ponto (180, 200) | ||
| − | pygame.draw.line(screen, (255, 0, 0), (30, 50), (180, 200)) | + | pygame.draw.line(screen, (255, 0, 0), |
| − | # Desenhamos um poligono | + | (30, 50), (180, 200)) |
| − | pygame.draw.polygon(screen, (0, 0, 255), [(200, 100), (300, 50), (400, 100), (350, 200), (250, 200)]) | + | |
| + | # Desenhamos um poligono com base no vetor de pontos passado como parâmetro. | ||
| + | pygame.draw.polygon(screen, (0, 0, 255), | ||
| + | [(200, 100), (300, 50), (400, 100), (350, 200), (250, 200)]) | ||
| + | |||
pygame.display.flip() | pygame.display.flip() | ||
| − | |||
pygame.quit() | pygame.quit() | ||
</syntaxhighlight>O código acima gera a representação visual mostrada abaixo. | </syntaxhighlight>O código acima gera a representação visual mostrada abaixo. | ||
| − | [[Arquivo:Linhas poligonos python.png|centro|miniaturadaimagem| | + | [[Arquivo:Linhas poligonos python.png|centro|miniaturadaimagem|Imagem resultado da visualização do programa em linguagem de programação python usando biblioteca pygame com uma linha e um polígono de cinco lados.]] |
| + | |||
| + | = Espaço Vetorial = | ||
| + | |||
| + | O espaço vetorial contém um conjunto de escalares e um conjunto de vetores. No caso do plano, ou espaço bidimensional, temos dois vetores, x e y, representando os eixos horizontal e vertical respectivamente respectivamente. Para representarmos um objeto no plano, precisamos de no mínimo um ponto, mas apenas um ponto pode não ser fácil de visualizar a não ser que coloquemos um marcador (+ ou x) no nosso gráfico. Para representar uma reta, usamos dois pontos e ligamos esses pontos com uma linha. A partir daí, com a conexão de pontos, podemos modelar objetos mais complexos. | ||
| + | |||
| + | <!-- | ||
| + | Código em C++ | ||
| + | |||
| + | <syntaxhighlight lang="c++"> | ||
| + | class Point2D { | ||
| + | public: | ||
| + | float x; | ||
| + | float y; | ||
| + | }; | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Código em Python | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | class Point2D: | ||
| + | def __init__(self, x: float, y: float): | ||
| + | self.x: float = x | ||
| + | self.y: float = y | ||
| + | </syntaxhighlight>O espaço tridimensional, por sua vez, é composto por três vetores, sendo eles o eixo x (horizontal), o eixo y (vertical) e, agora, o eixo z, que representa a profundidade Dessa forma, cada ponto é representado por (x, y, z). | ||
| + | |||
| + | <!-- | ||
| + | Código em C++ | ||
| + | |||
| + | <syntaxhighlight lang="c++"> | ||
| + | class Ponto3D { | ||
| + | public: | ||
| + | float x; | ||
| + | float y; | ||
| + | float z; | ||
| + | }; | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Código em Python | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | class Point3D: | ||
| + | def __init__(self, x: float, y: float, z: float): | ||
| + | self.x: float = x | ||
| + | self.y: float = y | ||
| + | self.z: float = z | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | = Desenhando um Triângulo em um espaço bidimensional = | ||
| + | |||
| + | O código abaixo cria um triângulo no plano (2 dimensões), ligando três pontos que estão conectados sequencialmente. A representação do ponto, já vimos acima e usamos uma estrutura de dados, no caso um objeto, com duas informações básicas, x e y, sendo atributos com tipo ponto flutuante. E para representar o triângulo, usamos um vetor de três pontos, ligando o ponto 0 com 1, 1 com 2 e 2 com 0 novamente para fechar o triângulo. | ||
| + | |||
| + | <!-- | ||
| + | Código em C++<syntaxhighlight lang="c++"> | ||
| + | #include <SFML/Graphics.hpp> | ||
| + | #include <SFML/Audio.hpp> | ||
| + | #include <iostream> | ||
| + | |||
| + | class Ponto | ||
| + | { | ||
| + | public: | ||
| + | float x; | ||
| + | float y; | ||
| + | Ponto (float _x, float _y) : x(_x), y(_y) {} | ||
| + | }; | ||
| + | |||
| + | int main() | ||
| + | { | ||
| + | sf::RenderWindow* app = new sf::RenderWindow(sf::VideoMode(800, 600, 32), "Triangulo 2D"); | ||
| + | |||
| + | Ponto* triangulo[3]; | ||
| + | triangulo[0] = new Ponto(50, 100); | ||
| + | triangulo[1] = new Ponto(100, 50); | ||
| + | triangulo[2] = new Ponto(150, 100); | ||
| + | |||
| + | while (app->IsOpened()) | ||
| + | { | ||
| + | sf::Event* event = new sf::Event(); | ||
| + | while (app->GetEvent(*event)) | ||
| + | { | ||
| + | if (event->Type == sf::Event::Closed) | ||
| + | { | ||
| + | app->Close(); | ||
| + | } | ||
| + | } | ||
| + | if (app->GetInput().IsKeyDown(sf::Key::Escape)) | ||
| + | { | ||
| + | return EXIT_SUCCESS; | ||
| + | } | ||
| + | |||
| + | app->Clear(sf::Color(255, 255, 255)); | ||
| + | for (int i = 0; i < 3; i++) | ||
| + | { | ||
| + | int j = i + 1; | ||
| + | if (j > 2) j = 0; | ||
| + | sf::Shape line = sf::Shape::Line(triangulo[i]->x, triangulo[i]->y, | ||
| + | triangulo[j]->x, triangulo[j]->y, | ||
| + | 1, sf::Color(0, 0, 0)); | ||
| + | app->Draw(line); | ||
| + | } | ||
| + | app->Display(); | ||
| + | } | ||
| + | return EXIT_SUCCESS; | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Código em Python | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | import pygame | ||
| + | |||
| + | class Point: | ||
| + | def __init__(self, x: float, y: float): # Nosso constructor do Ponto | ||
| + | self.x: float = x # Inicializamos o x | ||
| + | self.y: float = y # Inicializamos o y | ||
| + | |||
| + | screen = pygame.display.set_mode((800, 600)) # Inicializamos o pygame | ||
| + | triangle : list[Point] = [ # Criamos nosso triângulo | ||
| + | Point(50, 100), # Primeiro ponto | ||
| + | Point(100, 50), # Segundo ponto | ||
| + | Point(150, 100) # Terceiro ponto | ||
| + | ] | ||
| + | while True: # Iniciamos o laço do gameloop | ||
| + | for event in pygame.event.get(): # Testamos os eventos | ||
| + | if event.type == pygame.QUIT: # Se for o evento QUIT (botão x da janela) | ||
| + | sys.exit(0) # Fechamos o programa | ||
| + | elif event.type == pygame.KEYDOWN: # Se uma tecla for pressionada | ||
| + | if event.key == pygame.K_ESCAPE: # E essa tecla for ESC | ||
| + | sys.exit(0) # Fechamos o programa | ||
| + | |||
| + | screen.fill((255, 255, 255)) # Pintamos o fundo de branco | ||
| + | |||
| + | pygame.draw.line(screen, (0, 0, 0), # Criamos nossa primeira linha | ||
| + | (triangle[0].x, triangle[0].y), # conectando o ponto 0 | ||
| + | (triangle[1].x, triangle[1].y)) # com o ponto 1 | ||
| + | pygame.draw.line(screen, (0, 0, 0), # Criamos nossa segunda linha | ||
| + | (triangle[1].x, triangle[1].y), # conectando o ponto 1 | ||
| + | (triangle[2].x, triangle[2].y)) # ao ponto 2 | ||
| + | pygame.draw.line(screen, (0, 0, 0), # Criamos nossa terceira linha | ||
| + | (triangle[2].x, triangle[2].y), # conectando o ponto 2 | ||
| + | (triangle[0].x, triangle[0].y)) # ao ponto 0 | ||
| + | |||
| + | pygame.display.flip() # Trocamos a página de desenho | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | = Distância Euclidiana = | ||
| + | |||
| + | Muitas vezes iremos precisar da distância entre dois pontos. Visualmente é mais ou menos fácil identificar quando os pontos estão no eixo x ou y se tivermos boas marcações. Mas para um programa identificar não é bem assim. Para isso temos uma fórmula que encontra pra gente a distância entre dois pontos, essa distância, chamada de Distância Euclidiana, no caso do espaço bidimensional, é a raiz quadrada de x2 menos x1 elevado ao quadrado mais y2 menos y1 elevado ao quadrado. | ||
| + | |||
| + | |||
| + | <math> | ||
| + | \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} | ||
| + | </math> | ||
| + | = Funções Trigonométricas = | ||
| + | |||
| + | [[Image:Triangulo_angulos.png|Triangulo_angulos.png|thumb|Triângulo]] | ||
| + | |||
| + | Nas operações e transformações no plano ou espaço, precisaremos de algumas funções trigonométricas, então vamos fazer uma revisão aqui de um conteúdo lá do ensino médio. | ||
| + | |||
| + | Considere o triângulo da figura ao lado. | ||
| + | |||
| + | Para o ângulo α, chamamos de lado adjacente o lado que tem comprimento x, e de lado oposto o lado que tem comprimento y. O lado oposto ao ângulo reto, com comprimento h, é chamado de hipotenusa e satisfaz o Teorema de Pitágoras: | ||
| + | h<sup>2</sup> = x<sup>2</sup> + y<sup>2</sup> | ||
| + | As seis funções trigonométricas são definidas em relação ao ângulo α, como razões entre os comprimentos desses lados. | ||
| + | |||
| + | {| class="wikitable" style="margin: 1em auto 1em auto" | ||
| + | |+'''Funções Trigonométricas''' | ||
| + | ! Nome da Função !! Definição | ||
| + | |- | ||
| + | ! seno | ||
| + | | sen α = y / h | ||
| + | |- | ||
| + | ! cosseno | ||
| + | | cos α = x / h | ||
| + | |- | ||
| + | ! tangente | ||
| + | | tg α = y / h = sen α / cos α | ||
| + | |- | ||
| + | ! cossecante | ||
| + | | csc α = h / y = 1 / sen α | ||
| + | |- | ||
| + | ! secante | ||
| + | | sec α = h / x = 1 / cos α | ||
| + | |- | ||
| + | ! cotangente | ||
| + | | cot α = x / y = 1 / tg α | ||
| + | |} | ||
| + | |||
| + | As funções cossecante, secante e cotangente são raramente utilizadas na programação. Dessa forma, vamos estudar mais as funções de seno, cosseno e tangente. | ||
| + | |||
| + | O que torna as funções trigonométricas úteis é que para um dado ângulo α, as razões de comprimento dos lados de um triângulo retângulo contendo o ângulo α são sempre as mesmas. Assim, as funções seno, cosseno e tangente dependem apenas do ângulo α, e não do tamanho real do triângulo. | ||
| + | |||
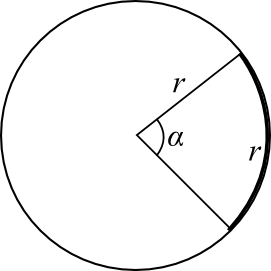
| + | [[Image:Circulo_angulos.png|Circulo_angulos.png|thumb|Em uma circunferência de raio r, um radiano é o ângulo α para o qual o arco circular subtendido por α tem um comprimento igual ao próprio r.]] | ||
| + | {| class="wikitable" style="margin: 1em auto 1em auto" | ||
| + | |+'''Valores de funções trigonométricas para ângulos comuns''' | ||
| + | ! radianos !! graus !! sen α !! cos α !! tg α | ||
| + | |- | ||
| + | | 0 | ||
| + | | 0º | ||
| + | | 0 | ||
| + | | 1 | ||
| + | | 0 | ||
| + | |- | ||
| + | | π/6 | ||
| + | | 30º | ||
| + | | 1/2 | ||
| + | | raiz(3)/2 | ||
| + | | raiz(3)/3 | ||
| + | |- | ||
| + | | π/4 | ||
| + | | 45º | ||
| + | | raiz(2)/2 | ||
| + | | raiz(2)/2 | ||
| + | | 1 | ||
| + | |- | ||
| + | | π/3 | ||
| + | | 60º | ||
| + | | raiz(3)/2 | ||
| + | | 1/2 | ||
| + | | raiz(3) | ||
| + | |- | ||
| + | | π/2 | ||
| + | | 90º | ||
| + | | 1 | ||
| + | | 0 | ||
| + | | indefinido | ||
| + | |} | ||
= Transformações Geométricas = | = Transformações Geométricas = | ||
Edição atual tal como às 13h52min de 16 de abril de 2025
Links Relacionados: Matemática e Física para Jogos, Usabilidade, Desenvolvimento Web, Mobile e Jogos
Introdução
- Geometria é a área da matemática que estuda as propriedades e relações das figuras no espaço.
- Fundamental para a computação gráfica, pois permite representar objetos de maneira estruturada.
- Facilita a manipulação e transformação de elementos gráficos em jogos e simulações.
Na computação gráfica, utilizamos conceitos geométricos para modelar cenários, animar personagens e criar efeitos visuais. As principais ferramentas para isso são as coordenadas cartesianas, transformações geométricas e o uso de matrizes para manipulação de objetos.
- Utilizamos escalares, pontos e vetores para representar quantidades, posições e direções.
- Através da combinação de operações sobre esses elementos podemos representar objetos geométricos e realizar o processamento necessário para a síntese de imagens.
Conceitos Básicos
- A base da geometria computacional são os pontos, linhas e polígonos.
- Pontos: elementos espaciais representados por coordenadas.
- Linhas: conectam dois pontos.
- Polígonos: formados por múltiplos segmentos.
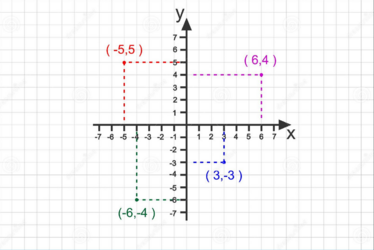
Coordenadas Cartesianas
- Um sistema de referência baseado em eixos:
- X e Y (em 2D) ou
- X, Y e Z (em 3D)
- Os eixos são usado para posicionar elementos gráficos.
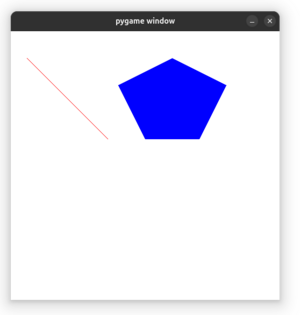
A seguir temos um exemplo de programa em python, com o uso da biblioteca pygame, para criar linhas e polígonos. Não estamos desenhando um ponto porque visualmente seria apenas um pixel. Usamos os pontos para criar as linhas e demais elementos.
pygame.init()
screen = pygame.display.set_mode((500, 500))
running = True
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
screen.fill((255, 255, 255))
# Desenhamos uma linha na tela, do ponto (30, 50) ao ponto (180, 200)
pygame.draw.line(screen, (255, 0, 0),
(30, 50), (180, 200))
# Desenhamos um poligono com base no vetor de pontos passado como parâmetro.
pygame.draw.polygon(screen, (0, 0, 255),
[(200, 100), (300, 50), (400, 100), (350, 200), (250, 200)])
pygame.display.flip()
pygame.quit()
O código acima gera a representação visual mostrada abaixo.
Espaço Vetorial
O espaço vetorial contém um conjunto de escalares e um conjunto de vetores. No caso do plano, ou espaço bidimensional, temos dois vetores, x e y, representando os eixos horizontal e vertical respectivamente respectivamente. Para representarmos um objeto no plano, precisamos de no mínimo um ponto, mas apenas um ponto pode não ser fácil de visualizar a não ser que coloquemos um marcador (+ ou x) no nosso gráfico. Para representar uma reta, usamos dois pontos e ligamos esses pontos com uma linha. A partir daí, com a conexão de pontos, podemos modelar objetos mais complexos.
class Point2D:
def __init__(self, x: float, y: float):
self.x: float = x
self.y: float = y
O espaço tridimensional, por sua vez, é composto por três vetores, sendo eles o eixo x (horizontal), o eixo y (vertical) e, agora, o eixo z, que representa a profundidade Dessa forma, cada ponto é representado por (x, y, z).
class Point3D:
def __init__(self, x: float, y: float, z: float):
self.x: float = x
self.y: float = y
self.z: float = z
Desenhando um Triângulo em um espaço bidimensional
O código abaixo cria um triângulo no plano (2 dimensões), ligando três pontos que estão conectados sequencialmente. A representação do ponto, já vimos acima e usamos uma estrutura de dados, no caso um objeto, com duas informações básicas, x e y, sendo atributos com tipo ponto flutuante. E para representar o triângulo, usamos um vetor de três pontos, ligando o ponto 0 com 1, 1 com 2 e 2 com 0 novamente para fechar o triângulo.
import pygame
class Point:
def __init__(self, x: float, y: float): # Nosso constructor do Ponto
self.x: float = x # Inicializamos o x
self.y: float = y # Inicializamos o y
screen = pygame.display.set_mode((800, 600)) # Inicializamos o pygame
triangle : list[Point] = [ # Criamos nosso triângulo
Point(50, 100), # Primeiro ponto
Point(100, 50), # Segundo ponto
Point(150, 100) # Terceiro ponto
]
while True: # Iniciamos o laço do gameloop
for event in pygame.event.get(): # Testamos os eventos
if event.type == pygame.QUIT: # Se for o evento QUIT (botão x da janela)
sys.exit(0) # Fechamos o programa
elif event.type == pygame.KEYDOWN: # Se uma tecla for pressionada
if event.key == pygame.K_ESCAPE: # E essa tecla for ESC
sys.exit(0) # Fechamos o programa
screen.fill((255, 255, 255)) # Pintamos o fundo de branco
pygame.draw.line(screen, (0, 0, 0), # Criamos nossa primeira linha
(triangle[0].x, triangle[0].y), # conectando o ponto 0
(triangle[1].x, triangle[1].y)) # com o ponto 1
pygame.draw.line(screen, (0, 0, 0), # Criamos nossa segunda linha
(triangle[1].x, triangle[1].y), # conectando o ponto 1
(triangle[2].x, triangle[2].y)) # ao ponto 2
pygame.draw.line(screen, (0, 0, 0), # Criamos nossa terceira linha
(triangle[2].x, triangle[2].y), # conectando o ponto 2
(triangle[0].x, triangle[0].y)) # ao ponto 0
pygame.display.flip() # Trocamos a página de desenho
Distância Euclidiana
Muitas vezes iremos precisar da distância entre dois pontos. Visualmente é mais ou menos fácil identificar quando os pontos estão no eixo x ou y se tivermos boas marcações. Mas para um programa identificar não é bem assim. Para isso temos uma fórmula que encontra pra gente a distância entre dois pontos, essa distância, chamada de Distância Euclidiana, no caso do espaço bidimensional, é a raiz quadrada de x2 menos x1 elevado ao quadrado mais y2 menos y1 elevado ao quadrado.
Funções Trigonométricas
Nas operações e transformações no plano ou espaço, precisaremos de algumas funções trigonométricas, então vamos fazer uma revisão aqui de um conteúdo lá do ensino médio.
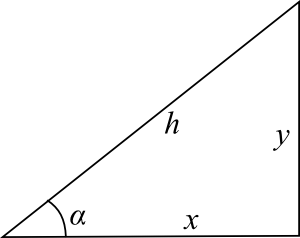
Considere o triângulo da figura ao lado.
Para o ângulo α, chamamos de lado adjacente o lado que tem comprimento x, e de lado oposto o lado que tem comprimento y. O lado oposto ao ângulo reto, com comprimento h, é chamado de hipotenusa e satisfaz o Teorema de Pitágoras:
h2 = x2 + y2
As seis funções trigonométricas são definidas em relação ao ângulo α, como razões entre os comprimentos desses lados.
| Nome da Função | Definição |
|---|---|
| seno | sen α = y / h |
| cosseno | cos α = x / h |
| tangente | tg α = y / h = sen α / cos α |
| cossecante | csc α = h / y = 1 / sen α |
| secante | sec α = h / x = 1 / cos α |
| cotangente | cot α = x / y = 1 / tg α |
As funções cossecante, secante e cotangente são raramente utilizadas na programação. Dessa forma, vamos estudar mais as funções de seno, cosseno e tangente.
O que torna as funções trigonométricas úteis é que para um dado ângulo α, as razões de comprimento dos lados de um triângulo retângulo contendo o ângulo α são sempre as mesmas. Assim, as funções seno, cosseno e tangente dependem apenas do ângulo α, e não do tamanho real do triângulo.
| radianos | graus | sen α | cos α | tg α |
|---|---|---|---|---|
| 0 | 0º | 0 | 1 | 0 |
| π/6 | 30º | 1/2 | raiz(3)/2 | raiz(3)/3 |
| π/4 | 45º | raiz(2)/2 | raiz(2)/2 | 1 |
| π/3 | 60º | raiz(3)/2 | 1/2 | raiz(3) |
| π/2 | 90º | 1 | 0 | indefinido |
Transformações Geométricas
- As transformações geométricas são as alterações na posição, tamanho e orientação de objetos gráficos. As principais são:
- Translação: Deslocamento de um objeto sem alterar sua forma.
- Rotação: Giro de um objeto em torno de um ponto específico.
- Escala: Aumento ou redução do tamanho de um objeto.
|