Mudanças entre as edições de "Vetores e Trigonometria"
| (9 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
| + | |||
Links Relacionados: [[Matemática e Física para Jogos]], [[Jogos Digitais]] | Links Relacionados: [[Matemática e Física para Jogos]], [[Jogos Digitais]] | ||
| Linha 4: | Linha 5: | ||
= Descrição = | = Descrição = | ||
| − | Na Computação Gráfica | + | Na Computação Gráfica — especialmente nos jogos digitais que utilizam esse recurso para criar apresentações visuais e permitir a interação com o ambiente — é comum o uso de grandezas vetoriais, como a direção e força do vento, a gravidade ou a direção para onde um personagem está olhando. |
| − | |||
| − | |||
| − | <center>[[ | + | Essas informações são representadas por vetores, que indicam tanto a direção quanto a intensidade (ou módulo) de uma ação. Um vetor possui características como sentido, direção e magnitude, sendo geralmente representado graficamente por uma seta.<center>[[Arquivo:Vetores.png|alt=|centro|commoldura|À esquerda temos uma seta diagonal apontando para em cima à direita. No meio uma seta vertical menor apontando para baixo e à direita uma seta horizontal maior apontando para a esquerda.]]</center>O código fonte da aula de Vetores está no github com um exemplo de jogo digital chamado [https://github.com/saulopz/vetorando vetorando]. |
= Características dos Vetores = | = Características dos Vetores = | ||
| − | + | Para representar e caracterizar nossos vetores, precisamos de informações como o tamanho, a direção e o sentido. E graficamente é uma seta que tem o ponto de origem, que é o ponto (0, 0) dela, e o ponto destino que é a ponta de uma seta, que representa as informações do vetor.<center>[[Arquivo:Vetores_representacao.png|alt=|centro|commoldura|Gráfico bidimensional com os eixos x e y e um vetor saindo do ponto (0, 0) até (4, 3), dando o deslocamento de x e y.]]</center> | |
| − | <center>[[ | ||
* '''Tamanho''': é a intensidade. É também chamado de magnitude; | * '''Tamanho''': é a intensidade. É também chamado de magnitude; | ||
| Linha 30: | Linha 28: | ||
= Representação na Programação = | = Representação na Programação = | ||
| − | No C++, python ou no Java, esses valores virariam variáveis float | + | No C++, python ou no Java, esses valores virariam variáveis float. Abaixo temos a representação, em linguagem de programação, da estrutura de dados de um ponto. No caso, um ponto no plano, espaço bidimensional, representado por duas variáveis de ponto flutuante x e y. A origem é sempre zero, então não é necessário representar. |
| + | <!-- | ||
Código em C++ | Código em C++ | ||
| Linha 43: | Linha 42: | ||
Vector2D(float _x, float _y) : x(_x), y(_y) {} | Vector2D(float _x, float _y) : x(_x), y(_y) {} | ||
}; | }; | ||
| − | </syntaxhighlight>Código em Python<syntaxhighlight lang="python3"> | + | </syntaxhighlight> |
| − | class | + | |
| + | Código em Python | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | class Vector2D: | ||
def __init__(self, x: float, y: float): | def __init__(self, x: float, y: float): | ||
self.x: float = x | self.x: float = x | ||
| Linha 52: | Linha 55: | ||
== Tamanho == | == Tamanho == | ||
| − | Para encontrarmos o tamanho, utilizamos a fórmula | + | Para encontrarmos o tamanho, utilizamos a fórmula da Distância Euclidiana apresentada na última aula. Transcrevendo-a em código de programação, temos: |
| − | + | <!-- | |
Código em C++ | Código em C++ | ||
| Linha 62: | Linha 65: | ||
return sqrt((x * x) + (y * y)); | return sqrt((x * x) + (y * y)); | ||
} | } | ||
| − | </syntaxhighlight>Código em Python<syntaxhighlight lang="python3"> | + | </syntaxhighlight> |
| + | |||
| + | Código em Python | ||
| + | --> | ||
| + | |||
| + | <syntaxhighlight lang="python3"> | ||
def size(self) -> float: | def size(self) -> float: | ||
return math.sqrt((self.x * self.x) + (self.y * self.y)) | return math.sqrt((self.x * self.x) + (self.y * self.y)) | ||
| Linha 71: | Linha 79: | ||
Também podemos utilizar operações de soma de vetores. Por exemplo: | Também podemos utilizar operações de soma de vetores. Por exemplo: | ||
| − | <center>[[ | + | <center>[[Arquivo:Vetores_soma.png|alt=|centro|commoldura|Imagem de duas operações de vetores, obtendo o resultado da soma de um vetor a e um vetor b.]]</center> |
| + | <!-- | ||
Com o código em C++: | Com o código em C++: | ||
| − | <syntaxhighlight lang=c | + | <syntaxhighlight lang="c++"> |
Vector2D Vector2D::operator +(const Vector2D& other) const { | Vector2D Vector2D::operator +(const Vector2D& other) const { | ||
return Vector2D(x + other.x, y + other.y); | return Vector2D(x + other.x, y + other.y); | ||
| Linha 85: | Linha 94: | ||
return *this; | return *this; | ||
} | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Código em Python | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | def add(self, other: "Vector2D") -> None: | ||
| + | self.x += other.x | ||
| + | self.y += other.y | ||
| + | |||
| + | @staticmethod | ||
| + | def sum(a: "Vector2D", b: "Vector2D") -> "Vector2D": | ||
| + | return Vector2D(a.x + b.x, a.y + b.y) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Um exemplo prático pode se ver na figura a seguir. Se quisermos representar a trajetória da bola, podemos somar o vetor gravidade ao vetor da trajetória. É possível também adicionar vetores como vento, por exemplo. | Um exemplo prático pode se ver na figura a seguir. Se quisermos representar a trajetória da bola, podemos somar o vetor gravidade ao vetor da trajetória. É possível também adicionar vetores como vento, por exemplo. | ||
| − | <center>[[ | + | <center>[[Arquivo:Vetores_chute.png|alt=|centro|commoldura|Na imagem, vemos um jogador de futebol chutando uma bola. Podemos perceber por meio da evolução dos vetores a balística acontecendo. Ao chutar, tempo 0, o vetor aponta diagonalmente para em cima a direita. Após 1 segundo, o vetor do chute é somado ao vetor gravidade, que é negativo verticalmente, apontando para baixo. Isso altera no sentido horário o ângulo do vetor do chute. A cada novo segundo, novamente o vetor gravidade é adicionado. Nesse sentido, a bola do jogador inicialmente está indo para frente e subindo, até que chega ao seu máximo para então descer em direção ao chão, mas ainda com uma velocidade horizontal à direita.]]</center> |
| − | Vetores também podem ser multiplicados por valores. Para tal, o código | + | Vetores também podem ser multiplicados por valores. Para tal, o código abaixo efetua essa operação: |
| − | <syntaxhighlight | + | <!-- |
| + | <syntaxhighlight lang="c++"> | ||
Vector2D Vector2D::operator *(float scalar) const { | Vector2D Vector2D::operator *(float scalar) const { | ||
return Vector2D(x * scalar, y * scalar); | return Vector2D(x * scalar, y * scalar); | ||
| Linha 103: | Linha 125: | ||
return *this; | return *this; | ||
} | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Código em Python | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | def multiply(self, other: "Vector2D") -> None: | ||
| + | self.x *= other.x | ||
| + | self.y *= other.y | ||
| + | |||
| + | @staticmethod | ||
| + | def multiply_vectors(a: "Vector2D", b: "Vector2D") -> "Vector2D": | ||
| + | return Vector2D(a.x * b.x, a.y * b.y) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
== Normalização == | == Normalização == | ||
| − | + | ara normalizar um vetor, ou seja, ajustar seu tamanho para que ele tenha comprimento 1, utilizamos a operação de normalização. Isso mantém a direção do vetor, mas reduz sua magnitude para 1. Esse vetor unitário pode, então, ser multiplicado por um valor escalar caso desejemos ajustar seu tamanho. | |
| − | <syntaxhighlight lang=c | + | Para normalizar, basta dividir as componentes x e y do vetor pelo seu comprimento. Veja o exemplo a seguir: |
| + | |||
| + | <!-- | ||
| + | <syntaxhighlight lang="c++"> | ||
Vector2D& Vector2D::normalize() { | Vector2D& Vector2D::normalize() { | ||
return (*this /= size()); | return (*this /= size()); | ||
} | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Cóidigo em Python: | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | def normalize(self) -> "Vector2D": | ||
| + | s: float = self.size() | ||
| + | return Vector2D(self.x / s, self.y / s) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Linha 119: | Linha 164: | ||
Se quisermos que o nosso atacante chute uma bola baseado no ângulo e na força, podemos criar um vetor com essas informações. | Se quisermos que o nosso atacante chute uma bola baseado no ângulo e na força, podemos criar um vetor com essas informações. | ||
| − | Se for dado um chute de ângulo 50 graus e a uma força 10, poderíamos chamar a função a baixo. Lembrando que | + | Se for dado um chute de ângulo 50 graus e a uma força 10, poderíamos chamar a função a baixo. Lembrando que o ângulo é em radianos (1 grau = PI/180 radianos). |
| + | |||
| + | <!-- | ||
| + | Código em C++ | ||
| − | <syntaxhighlight lang=c | + | <syntaxhighlight lang="c++"> |
Vector2D Vector2D::bySizeAndAngle(float size, float angle) { | Vector2D Vector2D::bySizeAndAngle(float size, float angle) { | ||
| − | + | float radians = angle * M_PI / 180.0f; // Converte graus para radianos | |
| + | return Vector2D(cos(radians) * size, sin(radians) * size); | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | + | Código em Python: | |
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | @staticmethod | ||
| + | def by_size_and_angle(size: float, angle: float) -> "Vector2D": | ||
| + | radians = math.radians(angle) # Converte graus para radianos | ||
| + | return Vector2D(math.cos(radians) * size, math.sin(radians) * size) | ||
| + | </syntaxhighlight> | ||
| − | <syntaxhighlight lang=c | + | Da mesma forma, podemos retornar qual o ângulo (em radianos) de um vetor por meio do arco tangente de x e y, conforme o código abaixo: |
| + | |||
| + | <!-- | ||
| + | <syntaxhighlight lang="c++"> | ||
float Vector2D::angle() const { | float Vector2D::angle() const { | ||
return atan2f(y, x); | return atan2f(y, x); | ||
} | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Código em Python: | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | def angle(self) -> float: | ||
| + | return math.atan2(self.y, self.x) # Retorna o ângulo em radianos | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Para facilitar, podemos fazer funções de conversão de radianos para graus e graus para radianos: | Para facilitar, podemos fazer funções de conversão de radianos para graus e graus para radianos: | ||
| − | <syntaxhighlight lang=c | + | <!-- |
| + | <syntaxhighlight lang="c++"> | ||
#define PI 3.1416 | #define PI 3.1416 | ||
| + | // Converte graus para radianos | ||
float grad2radians(float grad) { | float grad2radians(float grad) { | ||
| − | + | return (grad * PI) / 180; // Correção do fator de conversão | |
} | } | ||
| + | // Converte radianos para graus | ||
float radians2grad(float radians) { | float radians2grad(float radians) { | ||
| − | + | return (radians * 180) / PI; | |
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Também podemos rotacionar um vetor, utilizando a operação de rotação | + | Código em Python: |
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | # Converte graus para radianos | ||
| + | def grad2radians(grad: float) -> float: | ||
| + | return (grad * math.pi) / 180 | ||
| + | |||
| + | # Converte radianos para graus | ||
| + | def radians2grad(radians: float) -> float: | ||
| + | return (radians * 180) / math.pi | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Também podemos rotacionar um vetor, utilizando a operação de rotação (veremos melhor sobre a rotação nas próximas aulas). Contudo, nesse caso estamos trabalhando apenas com vetores, em que a posição não importa. Então estamos sempre tendo como base o eixo (0, 0) do vetor, não necessitando das operações de translação. | ||
| + | |||
| + | <!-- | ||
| + | <syntaxhighlight lang="c++"> | ||
| + | #define PI 3.1416 | ||
| − | |||
Vector2D& Vector2D::rotate(float angle) { | Vector2D& Vector2D::rotate(float angle) { | ||
| − | + | // Assumindo que 'angle' está em radianos. Se estiver em graus, converta para radianos: | |
| − | + | // angle = grad2radians(angle); // Se você quiser usar graus como entrada | |
| − | + | ||
| − | + | // Calculando o seno e o cosseno uma única vez para maior eficiência. | |
| − | + | float s = sin(angle); | |
| − | + | float c = cos(angle); | |
| − | + | ||
| − | + | // Fórmula de rotação | |
| − | + | float newX = (x * c) - (y * s); | |
| + | float newY = (x * s) + (y * c); | ||
| + | |||
| + | // Atualizando as coordenadas do vetor | ||
| + | x = newX; | ||
| + | y = newY; | ||
| + | |||
| + | // Retorna o próprio objeto para permitir encadeamento de métodos | ||
| + | // (por exemplo, v.rotate(...).rotate(...)) | ||
| + | return *this; | ||
} | } | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Código em Python: | ||
| + | --> | ||
| + | <syntaxhighlight lang="python3"> | ||
| + | def rotate(self, angle: float): | ||
| + | # Calculando o seno e o cosseno uma única vez | ||
| + | s = math.sin(angle) | ||
| + | c = math.cos(angle) | ||
| + | |||
| + | # Fórmula de rotação | ||
| + | new_x = (self.x * c) - (self.y * s) | ||
| + | new_y = (self.x * s) + (self.y * c) | ||
| + | |||
| + | # Atualizando as coordenadas do vetor | ||
| + | self.x = new_x | ||
| + | self.y = new_y | ||
| + | |||
| + | return self # Retorna o próprio objeto para encadeamento de métodos | ||
| + | # (ex: v.rotate(...).rotate(...)) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
== Ângulo entre dois vetores == | == Ângulo entre dois vetores == | ||
| − | Para encontrar o ângulo entre dois vetores, é utilizado o produto escalar, onde '''A ⋅ B''' é o produto escalar entre os pontos A e B: | + | Para encontrar o ângulo entre dois vetores, é utilizado o produto escalar, onde '''A ⋅ B''' é o produto escalar entre os pontos A e B, sendo que o produto escalar de A e B é igual à A<sub>x</sub> multiplicado por B<sub>x</sub> mais A<sub>y</sub> multiplicado por B<sub>y</sub>: |
<math> | <math> | ||
| Linha 173: | Linha 287: | ||
</math> | </math> | ||
| − | ou | + | ou, temos que o produto escalar dos vetores A e B é igual à magnitude de A (ou comprimento) multiplicado pela magnitude de B (ou comprimento) multiplicado pelo ângulo entre os vetores A e B. |
<math> | <math> | ||
| Linha 179: | Linha 293: | ||
</math> | </math> | ||
| − | Assim, podemos dizer que: | + | Assim, podemos dizer que o ângulo entre A e B é igual ao produto escalar de A e B dividido pelo Comprimento de A multiplicado pelo comprimento de B.: |
<math> | <math> | ||
| Linha 191: | Linha 305: | ||
</math> | </math> | ||
| − | ou, simplesmente: | + | ou seja, com os comprimentos de A e B sendo 1, ficamos simplesmente como sendo que o ângulo de A e B é o produto escalar de A e B: |
<math> | <math> | ||
| Linha 197: | Linha 311: | ||
</math> | </math> | ||
| − | Evitar o cálculo do tamanho reduz muito processamento, por isso é bom usar vetores normalizados para representar direções. | + | Evitar o cálculo do tamanho reduz muito processamento, por isso é bom usar vetores normalizados para representar direções. O método para o cálculo do produto escalar fica assim: |
| + | <!-- | ||
| + | Código em C++: | ||
| − | <syntaxhighlight lang=c | + | <syntaxhighlight lang="c++"> |
float Vector2D::dot(const Vector2D& other) const { | float Vector2D::dot(const Vector2D& other) const { | ||
return (x * other.x) + (y * other.y); | return (x * other.x) + (y * other.y); | ||
| Linha 205: | Linha 321: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | E o do ângulo entre os dois vetores unitários, assim: | + | Código em Python: |
| + | --> | ||
| + | |||
| + | <syntaxhighlight lang="python3"> | ||
| + | def dot(self, other: "Vector2D") -> float: | ||
| + | """ | ||
| + | Calcula o produto escalar entre este vetor e outro vetor. | ||
| + | Fórmula: A · B = Ax * Bx + Ay * By | ||
| + | """ | ||
| + | return (self.x * other.x) + (self.y * other.y) | ||
| + | </syntaxhighlight>E o do ângulo entre os dois vetores unitários, assim: | ||
| − | <syntaxhighlight lang=c | + | <!-- |
| + | <syntaxhighlight lang="c++"> | ||
float Vector2D::angleBetween(const Vector2D& other) const { | float Vector2D::angleBetween(const Vector2D& other) const { | ||
float dp = dot(other); | float dp = dot(other); | ||
| Linha 221: | Linha 348: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | = | + | Código em Python: |
| + | --> | ||
| + | |||
| + | <syntaxhighlight lang="python3"> | ||
| + | def angle_between(self, other: "Vector2D") -> float: | ||
| + | dp = self.dot(other) | ||
| + | size_product = self.size() * other.size() | ||
| + | # Evita divisão por zero caso um dos vetores tenha tamanho zero | ||
| + | if size_product == 0: | ||
| + | return 0.0 # ou talvez levantar exceção | ||
| + | |||
| + | # Garantir que o valor do produto escalar esteja entre -1 e 1 | ||
| + | cos_angle = dp / size_product | ||
| + | cos_angle = max(-1.0, min(1.0, cos_angle)) # clamp | ||
| + | |||
| + | # Calcular o ângulo em radianos | ||
| + | ang = math.acos(cos_angle) | ||
| − | + | # Produto vetorial 2D para decidir o sinal | |
| + | cross = self.x * other.y - self.y * other.x | ||
| + | # Retornar o ângulo positivo ou negativo dependendo do sinal do produto escalar | ||
| + | return ang if cross >= 0 else -ang | ||
| + | </syntaxhighlight> | ||
| − | + | = Exercícios = | |
| + | 1'''. Faça um programa com as seguintes características:''' | ||
* Clique na tela para definir o primeiro ponto (Ponto A) | * Clique na tela para definir o primeiro ponto (Ponto A) | ||
* Clique na tela para definir o segundo ponto (Ponto B) | * Clique na tela para definir o segundo ponto (Ponto B) | ||
Edição atual tal como às 12h03min de 19 de abril de 2025
Links Relacionados: Matemática e Física para Jogos, Jogos Digitais
Descrição
Na Computação Gráfica — especialmente nos jogos digitais que utilizam esse recurso para criar apresentações visuais e permitir a interação com o ambiente — é comum o uso de grandezas vetoriais, como a direção e força do vento, a gravidade ou a direção para onde um personagem está olhando.
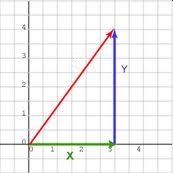
Essas informações são representadas por vetores, que indicam tanto a direção quanto a intensidade (ou módulo) de uma ação. Um vetor possui características como sentido, direção e magnitude, sendo geralmente representado graficamente por uma seta.
O código fonte da aula de Vetores está no github com um exemplo de jogo digital chamado vetorando.
Características dos Vetores
Para representar e caracterizar nossos vetores, precisamos de informações como o tamanho, a direção e o sentido. E graficamente é uma seta que tem o ponto de origem, que é o ponto (0, 0) dela, e o ponto destino que é a ponta de uma seta, que representa as informações do vetor.
- Tamanho: é a intensidade. É também chamado de magnitude;
- Direção: indica a inclinação do vetor no espaço;
- Sentido: mostra para onde o vetor está apontando;
Observação: vetores não possuem como propriedade a posição.
Vetores representam deslocamentos com sinal em cada eixo.
- Em 2 dimensões têm-se um valor para x e y.
- Em 3 dimensões, têm-se x, y e z.
- Em 4 dimensões, têm-se x, y, z e w.
Graficamente, representamos vetores como uma flecha. A posição da flecha não importa, desde que sua direção, tamanho e sentido sejam mantidos.
Representação na Programação
No C++, python ou no Java, esses valores virariam variáveis float. Abaixo temos a representação, em linguagem de programação, da estrutura de dados de um ponto. No caso, um ponto no plano, espaço bidimensional, representado por duas variáveis de ponto flutuante x e y. A origem é sempre zero, então não é necessário representar.
class Vector2D:
def __init__(self, x: float, y: float):
self.x: float = x
self.y: float = y
Tamanho
Para encontrarmos o tamanho, utilizamos a fórmula da Distância Euclidiana apresentada na última aula. Transcrevendo-a em código de programação, temos:
def size(self) -> float:
return math.sqrt((self.x * self.x) + (self.y * self.y))
Soma de Vetores
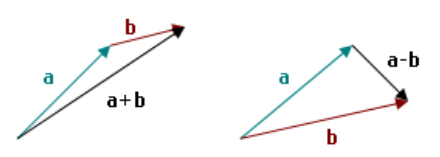
Também podemos utilizar operações de soma de vetores. Por exemplo:
def add(self, other: "Vector2D") -> None:
self.x += other.x
self.y += other.y
@staticmethod
def sum(a: "Vector2D", b: "Vector2D") -> "Vector2D":
return Vector2D(a.x + b.x, a.y + b.y)
Um exemplo prático pode se ver na figura a seguir. Se quisermos representar a trajetória da bola, podemos somar o vetor gravidade ao vetor da trajetória. É possível também adicionar vetores como vento, por exemplo.
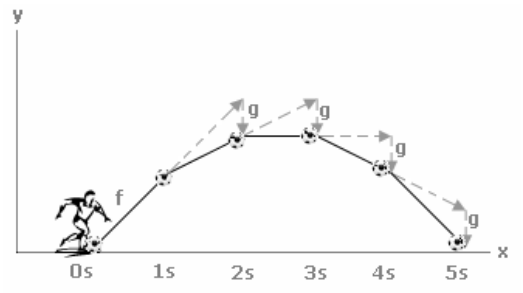
Vetores também podem ser multiplicados por valores. Para tal, o código abaixo efetua essa operação:
def multiply(self, other: "Vector2D") -> None:
self.x *= other.x
self.y *= other.y
@staticmethod
def multiply_vectors(a: "Vector2D", b: "Vector2D") -> "Vector2D":
return Vector2D(a.x * b.x, a.y * b.y)
Normalização
ara normalizar um vetor, ou seja, ajustar seu tamanho para que ele tenha comprimento 1, utilizamos a operação de normalização. Isso mantém a direção do vetor, mas reduz sua magnitude para 1. Esse vetor unitário pode, então, ser multiplicado por um valor escalar caso desejemos ajustar seu tamanho.
Para normalizar, basta dividir as componentes x e y do vetor pelo seu comprimento. Veja o exemplo a seguir:
def normalize(self) -> "Vector2D":
s: float = self.size()
return Vector2D(self.x / s, self.y / s)
Vetores e Ângulos
Se quisermos que o nosso atacante chute uma bola baseado no ângulo e na força, podemos criar um vetor com essas informações.
Se for dado um chute de ângulo 50 graus e a uma força 10, poderíamos chamar a função a baixo. Lembrando que o ângulo é em radianos (1 grau = PI/180 radianos).
@staticmethod
def by_size_and_angle(size: float, angle: float) -> "Vector2D":
radians = math.radians(angle) # Converte graus para radianos
return Vector2D(math.cos(radians) * size, math.sin(radians) * size)
Da mesma forma, podemos retornar qual o ângulo (em radianos) de um vetor por meio do arco tangente de x e y, conforme o código abaixo:
def angle(self) -> float:
return math.atan2(self.y, self.x) # Retorna o ângulo em radianos
Para facilitar, podemos fazer funções de conversão de radianos para graus e graus para radianos:
# Converte graus para radianos
def grad2radians(grad: float) -> float:
return (grad * math.pi) / 180
# Converte radianos para graus
def radians2grad(radians: float) -> float:
return (radians * 180) / math.pi
Também podemos rotacionar um vetor, utilizando a operação de rotação (veremos melhor sobre a rotação nas próximas aulas). Contudo, nesse caso estamos trabalhando apenas com vetores, em que a posição não importa. Então estamos sempre tendo como base o eixo (0, 0) do vetor, não necessitando das operações de translação.
def rotate(self, angle: float):
# Calculando o seno e o cosseno uma única vez
s = math.sin(angle)
c = math.cos(angle)
# Fórmula de rotação
new_x = (self.x * c) - (self.y * s)
new_y = (self.x * s) + (self.y * c)
# Atualizando as coordenadas do vetor
self.x = new_x
self.y = new_y
return self # Retorna o próprio objeto para encadeamento de métodos
# (ex: v.rotate(...).rotate(...))
Ângulo entre dois vetores
Para encontrar o ângulo entre dois vetores, é utilizado o produto escalar, onde A ⋅ B é o produto escalar entre os pontos A e B, sendo que o produto escalar de A e B é igual à Ax multiplicado por Bx mais Ay multiplicado por By:
ou, temos que o produto escalar dos vetores A e B é igual à magnitude de A (ou comprimento) multiplicado pela magnitude de B (ou comprimento) multiplicado pelo ângulo entre os vetores A e B.
Assim, podemos dizer que o ângulo entre A e B é igual ao produto escalar de A e B dividido pelo Comprimento de A multiplicado pelo comprimento de B.:
Onde |A| e |B| são respectivamente os tamanhos de A e B e α o ângulo que queremos calcular. Agora, note como o cálculo seria simplificado se A e B fossem vetores de tamanho 1:
ou seja, com os comprimentos de A e B sendo 1, ficamos simplesmente como sendo que o ângulo de A e B é o produto escalar de A e B:
Evitar o cálculo do tamanho reduz muito processamento, por isso é bom usar vetores normalizados para representar direções. O método para o cálculo do produto escalar fica assim:
def dot(self, other: "Vector2D") -> float:
"""
Calcula o produto escalar entre este vetor e outro vetor.
Fórmula: A · B = Ax * Bx + Ay * By
"""
return (self.x * other.x) + (self.y * other.y)
E o do ângulo entre os dois vetores unitários, assim:
def angle_between(self, other: "Vector2D") -> float:
dp = self.dot(other)
size_product = self.size() * other.size()
# Evita divisão por zero caso um dos vetores tenha tamanho zero
if size_product == 0:
return 0.0 # ou talvez levantar exceção
# Garantir que o valor do produto escalar esteja entre -1 e 1
cos_angle = dp / size_product
cos_angle = max(-1.0, min(1.0, cos_angle)) # clamp
# Calcular o ângulo em radianos
ang = math.acos(cos_angle)
# Produto vetorial 2D para decidir o sinal
cross = self.x * other.y - self.y * other.x
# Retornar o ângulo positivo ou negativo dependendo do sinal do produto escalar
return ang if cross >= 0 else -ang
Exercícios
1. Faça um programa com as seguintes características:
- Clique na tela para definir o primeiro ponto (Ponto A)
- Clique na tela para definir o segundo ponto (Ponto B)
- Desenhe uma linha entre o Ponto A e o Ponto B
- Informe na tela, em elementos tipo texto:
- a distância entre os pontos
- o ângulo do Ponto A para o Ponto B
- A cada novo clique, o Ponto B se tornará o Ponto A e o Ponto B será o novo local onde foi dado o clique. Redesenhe a linha entre A e B e refaça os cálculos e apresente-os na tela.
3. Faça um programa com as seguintes características:
- Desenhe do lado esquerdo da tela e abaixo um pequeno canhão.
- A movimentação do mouse para cima e para baixo altera o ângulo de tiro.
- A movimentação do mouse para a esquerda e direita altera a força do tiro.
- O clique do mouse efetua um disparo (represente o disparo com um ponto grande ou com uma imagem)
- Quando a bala do canhão cair, calcule a distância entre o canhão e a bala.
- Considere a gravidade como 9.8 m/s.
- Mostre na tela as informações de:
- Ângulo do tiro
- Força do tiro
- Distância percorrida pela bala do canhão.
4. No programa anterior, acrescente vento. Para isso:
- Crie um vetor de direção e velocidade do vento. Como estamos em um espaço bidimensional, considere apenas contra o canhão ou a favor do tiro do canhão (direita para esquerda ou esquerda para direita).
- Altere a velocidade do vento por meio das setas direcionais ( <- e -> ).
- Acrescente a informação da direção do vento e força.