Mudanças entre as edições de "Vetores e Trigonometria"
| Linha 31: | Linha 31: | ||
No C++, python ou no Java, esses valores virariam variáveis float: | No C++, python ou no Java, esses valores virariam variáveis float: | ||
| − | <-- | + | <!-- |
Código em C++ | Código em C++ | ||
Edição das 18h16min de 15 de abril de 2025
Links Relacionados: Matemática e Física para Jogos, Jogos Digitais
Descrição
Na Computação Gráfica, e consequentemente nos Games que se utiliza desse recurso para a apresentação e interação visual, são utilizadas algumas grandezas como direção e força do vento, gravidade, direção que um personagem está olhando, etc. Essa é descrita como uma grandeza vetorial.
Essas direções e intensidades são representadas por vetores. Estes possuem informações referentes a distância, sentido e tamanho, geralmente representados graficamente por setas.
Características dos Vetores
- Tamanho: é a intensidade. É também chamado de magnitude;
- Direção: indica a inclinação do vetor no espaço;
- Sentido: mostra para onde o vetor está apontando;
Observação: vetores não possuem como propriedade a posição.
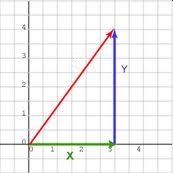
Vetores representam deslocamentos com sinal em cada eixo.
- Em 2 dimensões têm-se um valor para x e y.
- Em 3 dimensões, têm-se x, y e z.
- Em 4 dimensões, têm-se x, y, z e w.
Graficamente, representamos vetores como uma flecha. A posição da flecha não importa, desde que sua direção, tamanho e sentido sejam mantidos.
Representação na Programação
No C++, python ou no Java, esses valores virariam variáveis float:
class Vector2D:
def __init__(self, x: float, y: float):
self.x: float = x
self.y: float = y
Tamanho
Para encontrarmos o tamanho, utilizamos a fórmula definida na última aula. Transcrevendo-a em código, temos:
def size(self) -> float:
return math.sqrt((self.x * self.x) + (self.y * self.y))
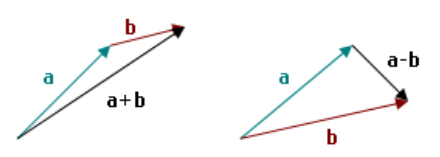
Soma de Vetores
Também podemos utilizar operações de soma de vetores. Por exemplo:
def add(self, other: "Vector2D") -> None:
self.x += other.x
self.y += other.y
@staticmethod
def sum(a: "Vector2D", b: "Vector2D") -> "Vector2D":
return Vector2D(a.x + b.x, a.y + b.y)
Um exemplo prático pode se ver na figura a seguir. Se quisermos representar a trajetória da bola, podemos somar o vetor gravidade ao vetor da trajetória. É possível também adicionar vetores como vento, por exemplo.
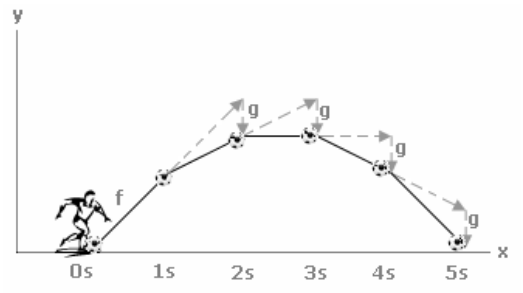
Vetores também podem ser multiplicados por valores. Para tal, o código abaixo efetua essa operação:
def multiply(self, other: "Vector2D") -> None:
self.x *= other.x
self.y *= other.y
@staticmethod
def multiply_vectors(a: "Vector2D", b: "Vector2D") -> "Vector2D":
return Vector2D(a.x * b.x, a.y * b.y)
Normalização
Para normalizar um vetor, ou seja, impor um tamanho a ele, utilizamos a operação de normalização. Isso reduz o tamanho do vetor para 1 (um). Este vetor normalizado pode então ser multiplicado por um escalar para obtermos tamanho desejado. Para normalizar um vetor, basta dividirmos x e y pelo tamanho do vetor. Segue o código:
def normalize(self) -> "Vector2D":
s: float = self.size()
return Vector2D(self.x / s, self.y / s)
Vetores e Ângulos
Se quisermos que o nosso atacante chute uma bola baseado no ângulo e na força, podemos criar um vetor com essas informações.
Se for dado um chute de ângulo 50 graus e a uma força 10, poderíamos chamar a função a baixo. Lembrando que o ângulo é em radianos (1 grau = PI/180 radianos).
@staticmethod
def by_size_and_angle(size: float, angle: float) -> "Vector2D":
radians = math.radians(angle) # Converte graus para radianos
return Vector2D(math.cos(radians) * size, math.sin(radians) * size)
Da mesma forma, podemos retornar qual o ângulo (em radianos) de um vetor por meio do arco-tangente de x e y, conforme o código abaixo:
def angle(self) -> float:
return math.atan2(self.y, self.x) # Retorna o ângulo em radianos
Para facilitar, podemos fazer funções de conversão de radianos para graus e graus para radianos:
# Converte graus para radianos
def grad2radians(grad: float) -> float:
return (grad * math.pi) / 180
# Converte radianos para graus
def radians2grad(radians: float) -> float:
return (radians * 180) / math.pi
Também podemos rotacionar um vetor, utilizando a operação de rotação vista na última aula. Contudo, nesse caso estamos trabalhando apenas com vetores, em que a posição não importa. Então estamos sempre tendo como base o eixo (0, 0) do vetor, não necessitando das operações de translação.
def rotate(self, angle: float):
# Calculando o seno e o cosseno uma única vez
s = math.sin(angle)
c = math.cos(angle)
# Fórmula de rotação
new_x = (self.x * c) - (self.y * s)
new_y = (self.x * s) + (self.y * c)
# Atualizando as coordenadas do vetor
self.x = new_x
self.y = new_y
return self # Retorna o próprio objeto para encadeamento de métodos
# (ex: v.rotate(...).rotate(...))
Ângulo entre dois vetores
Para encontrar o ângulo entre dois vetores, é utilizado o produto escalar, onde A ⋅ B é o produto escalar entre os pontos A e B:
Sendo que o produto escalar de A e B é igual à Ax multiplicado por Bx mais Ay multiplicado por By.
ou
Produto escalar dos vetores A e B é igual à magnitude de A (ou comprimento) multiplicado pela magnitude de B (ou comprimento) multiplicado pelo ângulo entre os vetores A e B.
Assim, podemos dizer que:
O ângulo entre A e B é igual ao produto escalar de A e B dividido pelo Comprimento de A multiplicado pelo comprimento de B.
Onde |A| e |B| são respectivamente os tamanhos de A e B e α o ângulo que queremos calcular. Agora, note como o cálculo seria simplificado se A e B fossem vetores de tamanho 1:
ou seja, com os comprimentos de A e B sendo 1, ficamos simplesmente com:
O ângulo de A e B é o produto escalar de A e B
Evitar o cálculo do tamanho reduz muito processamento, por isso é bom usar vetores normalizados para representar direções. O método para o cálculo do produto escalar fica assim:
def dot(self, other: "Vector2D") -> float:
"""
Calcula o produto escalar entre este vetor e outro vetor.
Fórmula: A · B = Ax * Bx + Ay * By
"""
return (self.x * other.x) + (self.y * other.y)
E o do ângulo entre os dois vetores unitários, assim:
def angle_between(self, other: "Vector2D") -> float:
dp = self.dot(other)
size_product = self.size() * other.size()
# Evita divisão por zero caso um dos vetores tenha tamanho zero
if size_product == 0:
return 0.0 # ou talvez levantar exceção
# Garantir que o valor do produto escalar esteja entre -1 e 1
cos_angle = dp / size_product
cos_angle = max(-1.0, min(1.0, cos_angle)) # clamp
# Calcular o ângulo em radianos
ang = math.acos(cos_angle)
# Produto vetorial 2D para decidir o sinal
cross = self.x * other.y - self.y * other.x
# Retornar o ângulo positivo ou negativo dependendo do sinal do produto escalar
return ang if cross >= 0 else -ang
Exercícios
1. Faça um programa com as seguintes características:
- Clique na tela para definir o primeiro ponto (Ponto A)
- Clique na tela para definir o segundo ponto (Ponto B)
- Desenhe uma linha entre o Ponto A e o Ponto B
- Informe na tela, em elementos tipo texto:
- a distância entre os pontos
- o ângulo do Ponto A para o Ponto B
- A cada novo clique, o Ponto B se tornará o Ponto A e o Ponto B será o novo local onde foi dado o clique. Redesenhe a linha entre A e B e refaça os cálculos e apresente-os na tela.
3. Faça um programa com as seguintes características:
- Desenhe do lado esquerdo da tela e abaixo um pequeno canhão.
- A movimentação do mouse para cima e para baixo altera o ângulo de tiro.
- A movimentação do mouse para a esquerda e direita altera a força do tiro.
- O clique do mouse efetua um disparo (represente o disparo com um ponto grande ou com uma imagem)
- Quando a bala do canhão cair, calcule a distância entre o canhão e a bala.
- Considere a gravidade como 9.8 m/s.
- Mostre na tela as informações de:
- Ângulo do tiro
- Força do tiro
- Distância percorrida pela bala do canhão.
4. No programa anterior, acrescente vento. Para isso:
- Crie um vetor de direção e velocidade do vento. Como estamos em um espaço bidimensional, considere apenas contra o canhão ou a favor do tiro do canhão (direita para esquerda ou esquerda para direita).
- Altere a velocidade do vento por meio das setas direcionais ( <- e -> ).
- Acrescente a informação da direção do vento e força.