Perspectiva ou Projeção Cônica
Afluentes: Computação Gráfica
Introdução
Para representarmos um espaço tridimensional — tal como percebido pelos olhos humanos — em um plano bidimensional, como a tela do computador, recorremos a uma das mais importantes descobertas do mundo das artes: a perspectiva.
Desenvolvida a partir de análises visuais e necessidades construtivas, a projeção em perspectiva surge durante o Renascimento, na busca por soluções geométricas para a construção da cúpula da Catedral de Florença, pelo arquiteto italiano Filippo Brunelleschi (1377–1446).
Essa técnica introduziu o realismo na pintura e no desenho, oferecendo uma maneira sistemática de representar a profundidade — ou melhor, a ilusão dela — sobre superfícies planas.
A projeção perspectiva produz uma imagem visualmente realista, embora não preserve as medidas reais dos objetos, pois executa uma transformação dentro do espaço tridimensional para representar a cena a partir de um ponto de observação a uma distância finita.
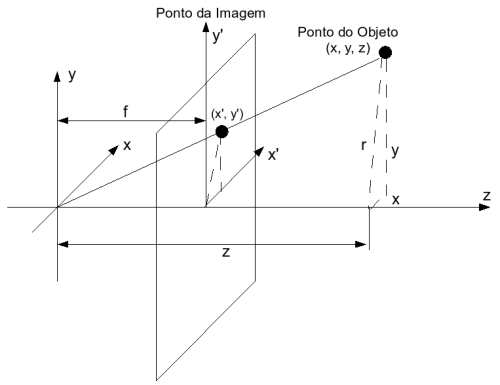
Na projeção perspectiva, as coordenadas dos pontos projetados são obtidas pela intersecção dos raios projetores com o plano de projeção, conforme ilustrado na Figura 1.
Termos
Sendo que:
- (x, y, z): coordenadas de um ponto no espaço 3D (a cena que está sendo projetada).
- f: a distância focal, que representa o quão longe está o plano da imagem do centro da projeção (o "olho" da câmera).
- (x′,y′): coordenadas do ponto projetado no plano da imagem, ou seja, no plano 2D.
- z é a distância do observador até o ponto original;
Ao aplicarmos o ponto do objeto no plano da imagem, iremos criar o ponto de projeção. Dessa forma, estamos aplicando uma transformação do espaço tridimensional para o espaço bidimensional.
Interpretação
Imagine que a câmera está olhando na direção do eixo Z, com o plano de projeção paralelo ao plano XY, colocado a uma distância f do centro (em z = f). O ponto 3D é então projetado em linha reta até esse plano.
Dessa forma, temos que x' dividido por x é igual a f dividido por x que implica em x' é igual a f dividido por z, multiplicado por x.
Logo, para encontrar o x' que é a representação no plano do x do espaço 3D, usamos a fórmula x' = f dividido por z, multiplicado por x:
E o mesmo se aplica a y ou seja, y' é igual a f dividido por z, multiplicado por y:
O z aqui é crucial — ele representa a profundidade. Quanto mais longe o objeto estiver (maior z), menor ele aparecerá na imagem — exatamente como nossos olhos percebem o mundo. Uma verdadeira dança de escala baseada na profundidade.
Formalizando mais...
Podemos ver essa projeção como uma transformação projetiva que leva um ponto 3D para 2D, ignorando a componente de profundidade na imagem. Em coordenadas homogêneas:
Para aplicarmos, fazemos uma operação de matrizes. Temos que a matriz vertical de três linhas e uma coluna, contendo x', y' e 1 é igual a matriz de três por quatro contendo na primeira linha: f, 0, 0 e 0, na segunda linha: 0, f, 0 e 0 e na terceira linha: 0, 0, 1 e 0, multiplicado pela matriz vertical de quatro por um contendo z, y, z e 1 da imagem 3D. Isso implica nas fórmulas para gerar x' e y' apresentadas anteriormente.
Essa abordagem é usada em gráficos computacionais, visão computacional, realidade aumentada, renderização 3D, etc.
E para implementar?
Tendo as equações já simplificadas, podemos agora aplicá-las na programação.
O exemplo a seguir apresenta, em forma de algoritmo, a função de transformação do espaço euclidiano tridimensional para sua projeção cônica na tela do nosso dispositivo computacional.
Distancia = 300
Elemento2 = Elemento
Para i = 0 até Quantidade_de_pontos fazer:
Elemento2[i].x = (Distancia / Elemento[i].z) * Elemento[i].x
Elemento2[i].y = (Distancia / Elemento[i].z) * Elemento[i].y
Fim para
Ou, em Python:
DISTANCIA = 300
def projetar_ponto(ponto):
x, y, z = ponto
fator = DISTANCIA / z
return (fator * x, fator * y)
elemento = [(x, y, z) for x, y, z in ...] # seus pontos 3D
elemento2 = [projetar_ponto(p) for p in elemento]
Com isso, criamos um novo conjunto de pontos Elemento2, que representa a projeção do objeto original (Elemento) no plano de visualização.
A partir deste ponto, não exibiremos mais o objeto original, mas sim sua representação projetada.
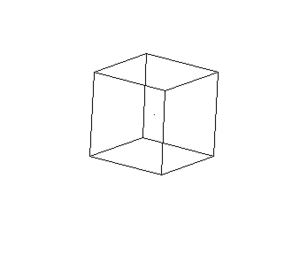
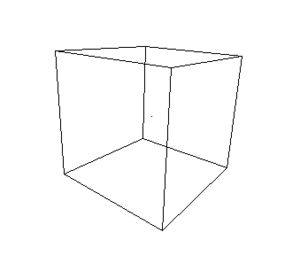
O resultado dessa transformação, aplicada a um cubo originalmente situado no espaço euclidiano (Figura 2), é apresentado na Figura 3, agora sob uma perspectiva central.
Implementação
Script cubo3d.py.
from __future__ import annotations
import sys
import math
import pygame
# Configuração
SPEED: float = 0.1
WIDTH: int = 800
HEIGHT: int = 600
Color_screen: pygame.Color = (255, 255, 255)
Color_line: pygame.Color = (0, 0, 0)
CONICAL: bool = False
DISTANCE: float = 300
# -------------------------
# Classe Point
# -------------------------
class Point:
def __init__(self, x: float, y: float, z: float):
self.x: float = x # vetor x
self.y: float = y # vetor y
self.z: float = z # vetor z
def copy(self) -> Point: # Cria uma copia do ponto
return Point(self.x, self.y, self.z)
# -------------------------
# Classe Cube
# -------------------------
class Cube:
def __init__(self, screen):
self.screen: pygame.display = screen # Referencia a screen do pygame
self.points: list[Point] = [ # Criacao dos pontos do cubo
Point(0, 0, 0),
Point(-50, -50, -50),
Point(+50, -50, -50),
Point(+50, +50, -50),
Point(-50, +50, -50),
Point(-50, -50, +50),
Point(+50, -50, +50),
Point(+50, +50, +50),
Point(-50, +50, +50),
]
self.translate(0, 0, 300) # Move para uma posicao inicial longe da tela
def translate(self, tx, ty, tz) -> None: # Translada o cubo
for p in self.points: # Para cada ponto executa a matriz de translacao
p.x += tx # Soma x a tx
p.y += ty # Soma y a ty
p.z += tz # Soma z a tz
def scale(self, sx, sy, sz) -> None: # Executa a escala no cubo
pivot = self.points[0].copy() # Cria uma copia do ponto pivo
self.translate(-pivot.x, -pivot.y, -pivot.z) # Translada para a origem com referencia ao pivo
for p in self.point: # Executa a matriz de escala para cada ponto
p.x *= sx
p.y *= sy
p.z *= sz
self.translate(pivot.x, pivot.y, pivot.z) # Translada da origem de volta ao pivo original
def rotate(self, angle, axis): # Executa a rotacao do cubo
angle = math.radians(angle) # Converter para radianos
pivot = self.points[0].copy() # Faz uma copia do ponto pivo
self.translate(-pivot.x, -pivot.y, -pivot.z) # Translada para a origem com referência ao pivo
for p in self.points: # Executa a matriz de rotacao em cada ponto e cada vetor
x, y, z = p.x, p.y, p.z
if axis == "x":
p.y = y * math.cos(angle) - z * math.sin(angle)
p.z = z * math.cos(angle) + y * math.sin(angle)
elif axis == "y":
p.x = x * math.cos(angle) - z * math.sin(angle)
p.z = z * math.cos(angle) + x * math.sin(angle)
elif axis == "z":
p.x = x * math.cos(angle) - y * math.sin(angle)
p.y = y * math.cos(angle) + x * math.sin(angle)
self.translate(pivot.x, pivot.y, pivot.z)
# Executa visualizacao da projecao conica / perspectiva se ativa
def perspective(self, p) -> Point:
if CONICAL and p.z != 0:
scale = DISTANCE / p.z
return Point(p.x * scale, p.y * scale, p.z)
return Point(p.x, p.y, p.z)
def line(self, p1, p2) -> None:
pygame.draw.line(self.screen, Color_line, (p1.x, p1.y), (p2.x, p2.y))
# Desenha o cubo
def draw(self) -> None:
p = []
for i in range(9):
point = self.perspective(self.points[i])
point.x += WIDTH / 2
point.y += HEIGHT / 2
p.append(point)
self.line(p[0], p[0]) # draw point over pivot
for i in range(3):
self.line(p[i + 1], p[i + 2])
self.line(p[i + 5], p[i + 5 + 1])
self.line(p[i + 1], p[i + 5])
self.line(p[4], p[1])
self.line(p[8], p[4])
self.line(p[5], p[8])
def change(self, move):
if move == "translate_left":
self.translate(-SPEED, 0, 0)
elif move == "translate_right":
self.translate(SPEED, 0, 0)
elif move == "translate_up":
self.translate(0, -SPEED, 0)
elif move == "translate_down":
self.translate(0, SPEED, 0)
elif move == "translate_front":
self.translate(0, 0, SPEED)
elif move == "translate_back":
self.translate(0, 0, -SPEED)
elif move == "rotate_y_left":
self.rotate(-SPEED, "y")
elif move == "rotate_y_right":
self.rotate(SPEED, "y")
elif move == "rotate_x_up":
self.rotate(SPEED, "x")
elif move == "rotate_x_down":
self.rotate(-SPEED, "x")
elif move == "rotate_z_right":
self.rotate(SPEED, "z")
elif move == "rotate_z_left":
self.rotate(-SPEED, "z")
def show_help(screen, font):
help = [
font.render("ESC: Fecha o programa", True, (200, 200, 200)),
font.render("A, D: Rotaciona no eixo X", True, (200, 200, 200)),
font.render("S, W: Rotaciona mo eixo Y", True, (200, 200, 200)),
font.render("Z, X: Rotaciona mo eixo Z", True, (200, 200, 200)),
font.render("Setas ESQUERDA, DIREITA: Translada mo eixo X", True, (200, 200, 200)),
font.render("Setas CIMA, BAIXO: Translada mo eixo Y", True, (200, 200, 200)),
font.render("Q, E: Translada no eixo Z", True, (200, 200, 200)),
font.render("C: Liga/desliga a projeção cônica", True, (200, 200, 200)),
]
help_pos_y = 10
for i in range(len(help)):
screen.blit(help[i], (10, help_pos_y))
help_pos_y += 25
def main():
global CONICAL
pygame.init()
screen = pygame.display.set_mode((WIDTH, HEIGHT))
font = pygame.font.SysFont(None, 22)
cube = Cube(screen)
cube.draw()
move = ""
while True:
for event in pygame.event.get():
if event.type == pygame.QUIT:
sys.exit(0)
elif event.type == pygame.KEYDOWN:
if event.key == pygame.K_LEFT:
move = "translate_left"
elif event.key == pygame.K_RIGHT:
move = "translate_right"
elif event.key == pygame.K_DOWN:
move = "translate_down"
elif event.key == pygame.K_UP:
move = "translate_up"
elif event.key == pygame.K_q:
move = "translate_back"
elif event.key == pygame.K_e:
move = "translate_front"
elif event.key == pygame.K_a:
move = "rotate_y_left"
elif event.key == pygame.K_d:
move = "rotate_y_right"
elif event.key == pygame.K_w:
move = "rotate_x_up"
elif event.key == pygame.K_s:
move = "rotate_x_down"
elif event.key == pygame.K_x:
move = "rotate_z_right"
elif event.key == pygame.K_z:
move = "rotate_z_left"
elif event.key == pygame.K_c:
CONICAL = not CONICAL
elif event.key == pygame.K_ESCAPE:
pygame.quit()
sys.exit(0)
elif event.type == pygame.KEYUP:
move = ""
cube.change(move)
screen.fill(Color_screen)
cube.draw()
show_help(screen, font)
pygame.display.flip()
if __name__ == "__main__":
main()